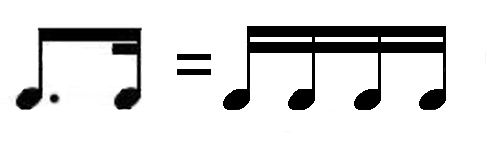|
   
   
   
   
   
   
   
   
   
Johann Sebastian Bach titkai
Három az Egyhez a Négyben
Az Aranymetszés
Visszatérünk Johann Sebastian Bach egyik legcsodálatosabb,
hegedűre alkotott művéhez, a második Partita utolsó tételéhez, a
Chaconne-hoz. Ebben a fejezetben a mű 3., 4., 5. és 6. variációjával
foglalkozunk. Lássuk a kottaképet!

89. ábra
A harmadik és a negyedik variáció teljesen megegyezik egymással a
harmadik ütem utolsó akkordjáig, majd a negyedik ütemek térnek el
egymástól. Ugyanez mondható el az ötödik és hatodik variációkról.
Ennek egyik oka: a világegyetemben minden létezési megnyilvánulás
azonosnak mondható addig a pillanatig, míg összehasonlítási lehetőség
nem áll fenn számára más Létezővel. A találkozások különbözősége
pedig meghatározza milyen változásokon mennek át maguk a Létezők és
a keletkezett létezési alakzatok.
A harmadik variáció 48 Hangból áll, a negyedik variációt szintén 48
Hang alkotja.
48+48= 96 Az Univerzum mintája. Mivel itt pontosan a felére osztotta a
96-os számot, a két pólusról beszélünk. Sokszor találkoztunk már a
96-os számmal, a 16. fejezetben, „A Bindu, az Ősvizek világa” című
írásomban olvasható erről a számról egy hosszabb időfizikai értékelés.
Ebben a két variációban találunk még 12 szünetet. 96+12=108
Ezt a számot is nagyon kedveljük, ő a Fény a Renum 11 szerint. Azonkívül
a Hunoknak ennyi népcsoportjuk van (volt), illetve a Tűz, a Víz, a
Levegő és a Föld Őselemeknek pontosan ennyi (Hang)- Helyre van szükségük
a „megszületésükhöz”. Ennek az elemzése a 17. fejezetben található.
(4x27=108)
Az ötödik és hatodik variációt 82 Hang alkotja, hozzájön a 14 szünet
=96
96+82=178 Hang + 26 szünet =204
Nézzük meg azokat az eredményeket a Renum 11-ben, amikkel még nem találkoztunk!
82= időmérő, bölcsek.
178= vándorol, felismerés, terembura, ősállapot, az időkapu.
204= alapvető, a lényeg tana, őstudat, dimenziós, a felemelkedő
Isten, a Merkaba titkai, az új Rend, maga a Létező, a teljes hit, istenáldás.
Mit rejt a fejezet címe?
Három az Egyhez a Négyben Az Aranymetszés=1017=felismerni hogy milyen
az Isten és hogy ki az Isten, a transzcendens ősvalóságra való ráirányulás,
az Isteni gondolatok visszaszerzése, szentségi viszonyba kerülni Jézussal,
az igaz emberben maradéktalanul megvalósult Isten titka, Hol áldás ott
Isten Hol Isten ott szükség nincsen, a leegyszerűsítés elvének maradéktalan
megfogalmazása, a beavatás célja a lét eredeti egységének teljes
helyreállítása, a legegyszerűbb megoldások alkalmazásának elvét jól
megérteni, a tökéletes egyesítés elvét hiánytalanul megérteni, Názáreti
Jézus jelenléti módja a szent ostyában.
Most vizsgáljuk meg a variációk időértékét. A legkisebb ritmusérték
a 32-ed, így ő lesz az alapmérték. A Terek és Antiterek összege 32.
Három negyedes ütemmutatóval megy végig a darab (korábban elemeztük),
ahol a negyed az alap. Egy negyedben 8 (Fény) 32-ed érték van, három
negyedben (ennyi negyed szerepel egy ütemben) 24 (Kerubok száma) darab
32-ed érték szerepel és egy variációban 12 negyed számolható össze:
12x8= 96, vagyis a Minta.
96x32= 3072
Ez a szám az egyes variációk időértéke. Az RV=4,16 egy 30 fokos szöget
zár be, a 72 pedig a Kerubok, a nagy lelkek száma.
Mit mond a Renum 11?
3072=A világegyetemben jelen levő részecskék mozgása hozza létre a
nullpont mezőt, s egyfajta öngerjesztő visszacsatolási hurok működik
a kozmoszban.
Az Aranymetszés ritmusa
Ha jobban megnézzük ennek a négy variációnak a kottaképét, észrevesszük,
hogy egy érdekes ritmusképlet kíséri, alapozza megszakadás nélkül
az egész zenei folyamatot. Minden zenei Hangot, akkordot, ritmust, ami
valamilyen módon össze van kötve egymással, minden esetben együtt
kell értelmezni. Ez persze nem zárja ki, hogy van kötődése másfajta
alakzatokhoz és ez logikus is, hiszen minden mindennel összefüggésben
van (minden Istenből jött létre és Őhozzá tér vissza), de ahhoz,
hogy az egész lényegét átlássuk, a legkisebb részleteket kell először
megfejteni.
Ez a ritmusképlet kettő Hangból áll, az első Hang mögött egy pont
van és a vele összekötött második Hang száránál, az összekötési
vonal alatt találunk egy másik rövidke vonalat. Az értelmezésnél a képletben
előforduló legkisebb egységet kell alapnak venni, így az itt jelenlevő
két Hang négy tizenhatodot tartalmaz.
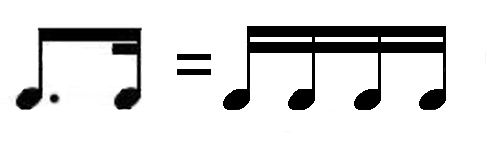
90. ábra
Az első értékhez három darab tizenhatod tartozik, a másodikhoz pedig
egy darab tizenhatod érték. A neve ennek a ritmusképletnek a kis nyújtott
ritmus. Mi a véleménye a Renum 11-nek erről a ritmusról?
Kis nyújtott ritmus= 572= a számok könyvének megtalálása, a szabadságba
vezető út, az Istenmegértés képessége, az abszolút szabadság,
igazságfeltáró kódrendszer, az eredeti teremtés lényege, az Isten által
adott kegyelem, a legmagasabb rendű ember felemelkedése a végtelenbe,
az univerzum áthangolása, Isten országa bennetek van, a titkos tudomány
megértése, az élet könyvének közepe, Isten titokzatos léte, az
Isteni kulcsinformációk ismerője, az igazság feltárása, hol van az
isteni kiindulópont, az Isten templomának felépítése.
Amikor kódfejtésről beszélünk, a rendelkezésünkre álló adatokat
kell másféleképpen értelmeznünk anélkül, hogy az eredeti képlet
tulajdonságait megváltoztatnánk. Az egyik lehetőség a geometria. Négy
egyenlő értékű tizenhatod, négy egyenlő oldalú alakzat. Ez ugye nem
lehet más, mint a négyzet. Ennek a ritmusképletnek az értelmezése:
egy negyedben, egy négyzeten belül van négy egyforma rész, ahol
megmutatkozik a három az egyhez való kapcsolat úgy, hogy értelmezhető
legyen a 3, az 1 és a 4. Az, hogy a Pi kezdő számai jöttek ki belőle
csak „véletlen”.
Vagyis a négyzetet fel kell osztani négy egyforma, a négyzetet teljesen
kitöltő geometriai alakzatra, ahol már a legkisebb rész is magában
hordoz három különböző adatot, illetve a többiekhez való viszonyítási
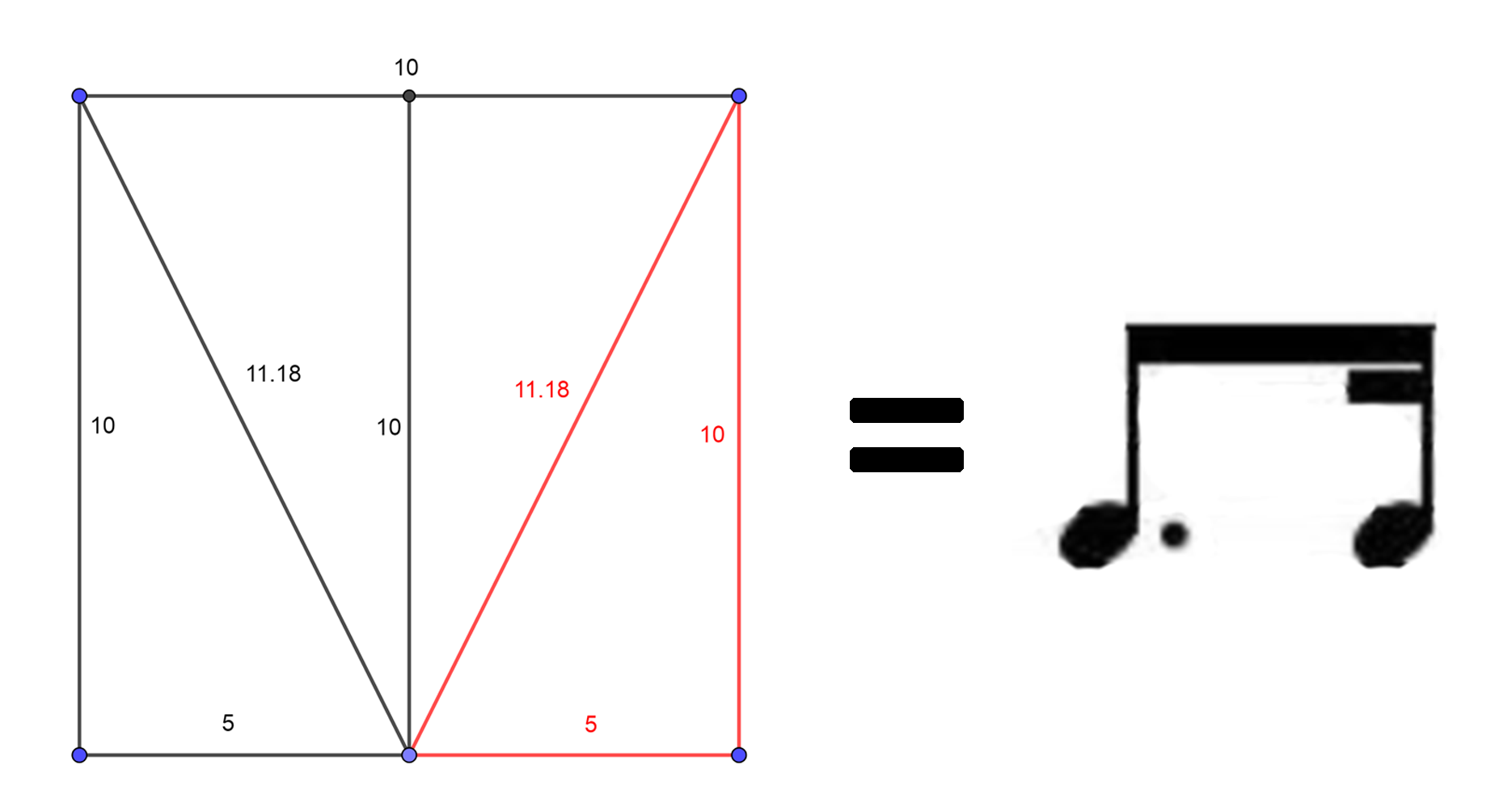
kapcsolatát. Ez nem lehet más, mint 4 egyforma háromszög, három különböző
oldalnagysággal.
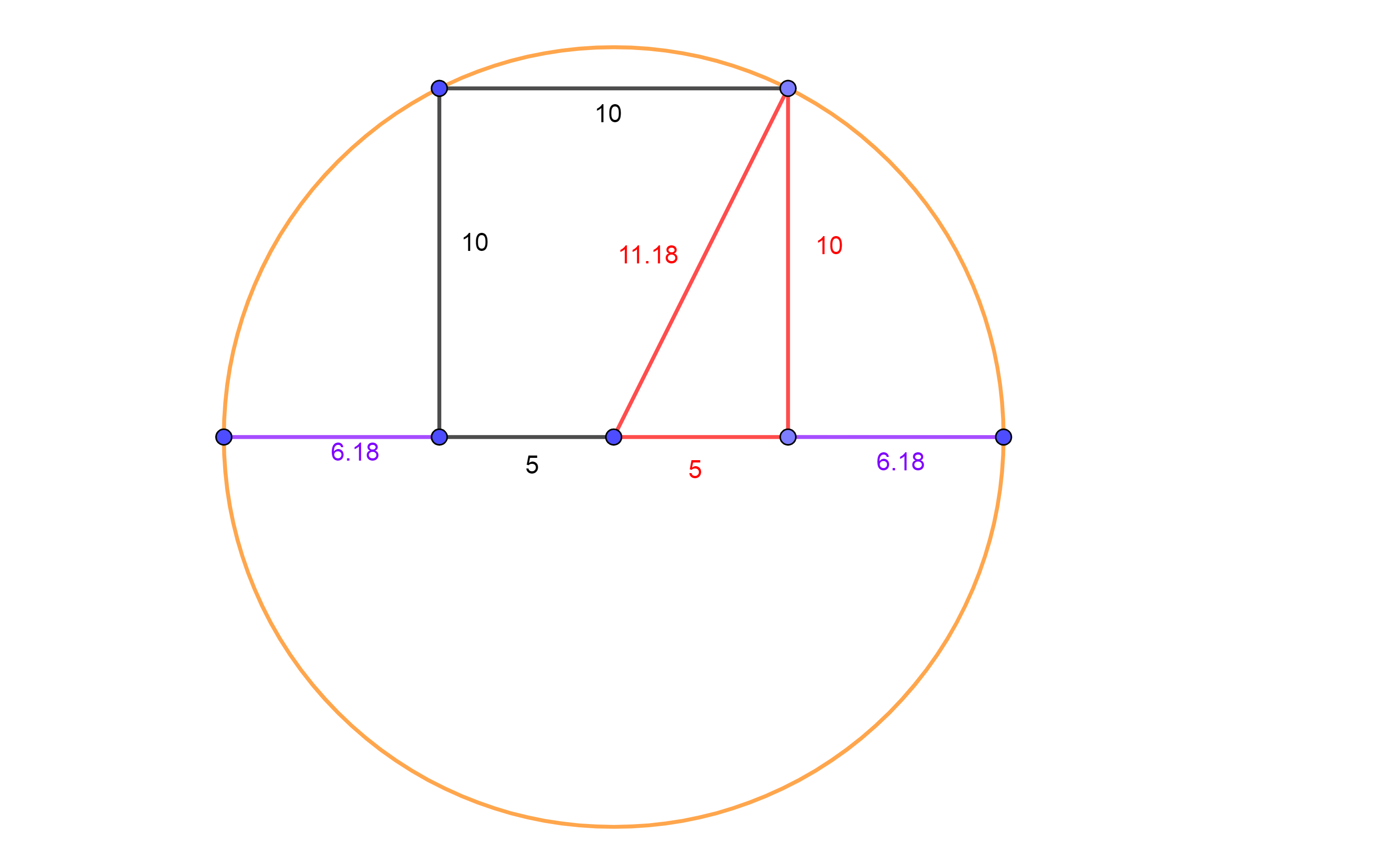
91. ábra
Az első kottajegyhez három darab háromszög tartozik, a második
kottajegyhez pedig egy háromszög tartozik.
Tehát a legkisebb alakzata ennek az ábrázolási módnak, a háromszög,
megmutat három különböző oldalt (adatot), az ábránkon ez 5, 10 és
11,18-nak felel meg. Az, hogy háromszöget alkot, megmutatja az ő arányát
a másik három háromszöghöz (három az egyhez) és az, hogy összesen
négy darab van belőle, megmutatja a négyben az egy viszonyát. Gondolom
már mindenki kitalálta, hogy innen ered a fejezet címe is!
A következő ábra már önmagáért beszél, ahol a négyzeten belül
pontosan úgy ábrázoljuk a háromszögeket, ahogyan a ritmusképletben,
hármat egyben és a hozzákapcsolódó egyet mellette.
92. ábra
A Teremtő által megalkotott ritmusképletben, megfelelő ábrázolási módon
megkapjuk az univerzum egyik legfontosabb szabályának az adatait, amiből
a világ minden teremtményének a felépülési struktúrájának
viszonyait mutathatjuk, számolhatjuk, teremthetjük meg, azaz az
aranymetszési arányt.
A négyzet oldalainak meghosszabbításával, illetve a háromszög
leghosszabb oldala, ami az aranymetszési kör, „gömb” sugarát
alkotja, megalkothatjuk a legbonyolultabb aranymetszési ábrázolásokat.
Én csak az első lépést tettem meg, mert innen, hogy mit építünk tovább,
már a teremtmények fantáziájára van bízva. Természetesen a négyzet
bármelyik oldaláról lehet köröket, „gömböket” alkotni a végtelenségig,
amik újabb „négyzeteket”, „gömböket”, „spirálokat”,
„fraktálokat”, világokat hoznak létre.
Most nézzük meg a ritmusképlet két tagjának az egymáshoz való
viszonyát egy egyszerű osztással. Egy a háromhoz= 1:3= 0,
33333333333……..
Minden aranymetszési kapcsolatnál jelen van Jézus Urunk, a Teremtő Fiú,
Ő az Első leágazás a Teremtő Forrásból, Ő aki Elsőnek keletkezett
és Ő, aki utolsónak olvad vissza a Teremtő Forrásba.
Az aranymetszés ritmusképlete végig jelen van a mostani fejezetben
vizsgált négy variációban. Ha jobban megnézzük a kottát, találunk
egy pár picit eltérő ritmusképletet az „eredeti” ritmusképlettől.

93. ábra
Itt ugye kettő aránylik a háromhoz. 2:3= 0, 6666666666……
Igen, Lucifer jelenléte is nagyon fontos az univerzumban, hiszen tudása
hatalmas és Teremtő Atyánk szeretete Őt is átkarolja. Számoljuk össze
hány alkalommal jelenik meg ez a ritmusképlet! Pontosan nyolc
alkalommal. Lucifer, a Fényhozó.
Ebben a ritmusképletben a legkisebb ritmus a 32-ed érték, ami a második
és a harmadik hangérték. Az első hangérték 32-ed értékekben számolva
hat darab 32-ed értéket ad ki. 2:6= 0, 3333333333…
Jézus Őbenne is jelen van, Jézus nélkül Ő sem létezne, Jézus tudása,
Jézus szeretete nélkül Ő sem élne!
Most számoljuk meg összesen hány alkalommal jelennek meg ebben a négy
variációban ezek a ritmusképletek (ahol több szólamban egyszerre
szerepel ugyanaz a képlet, természetesen külön számolom).
14+15+15+12= 56
Az 56-os számról nekem az jut az eszembe, hogy ötről a hatra, vagyis a
Téridő létrejötte, ahol már feltűnik az aranymetszés rendszere.
Osszuk el az 56-os számot a Fény számaival. 56:7= 8 és 56:8= 7
Hétről a nyolcra, vagyis a Fény létrejöttében is fontos szerepet játszik
az aranymetszés.
Az akkordok területe és aranymetszési láncsorozatai
A négy variációnak összesen 28 Hanghely szükségeltetik a zenei kotta
létrejöttéhez. Ebből 7 Hely üresen marad, de ettől ők még léteznek.
Tehát 21 betöltött Hely van. Létrehoztam egy kört, amit egymástól
egyforma távolságban levő 28 pont alkot. Ha valaki később ezzel tovább
dolgozik mindenképpen gömb formában gondolkodjon, mert közelebb visz a
megoldásokhoz. Minden pont egy Hang Helyét jelöli és mivel a Hangok
egyenlő (félhang) távolságra helyezkednek el egymástól, így a
pontok is egyenlő távolságban vannak egymástól. Mivel „bezárul”
a kör, a legmélyebb Hang mellé az itt előforduló legmagasabb Hang kerül.
Az egymáshoz tartozó Hangok, akkordok alkotják a különböző
geometriai alakzatokat úgy, hogy a kört alkotó megfelelő Hangokat összekötöttem
egymással. Mutatok kettő példát!
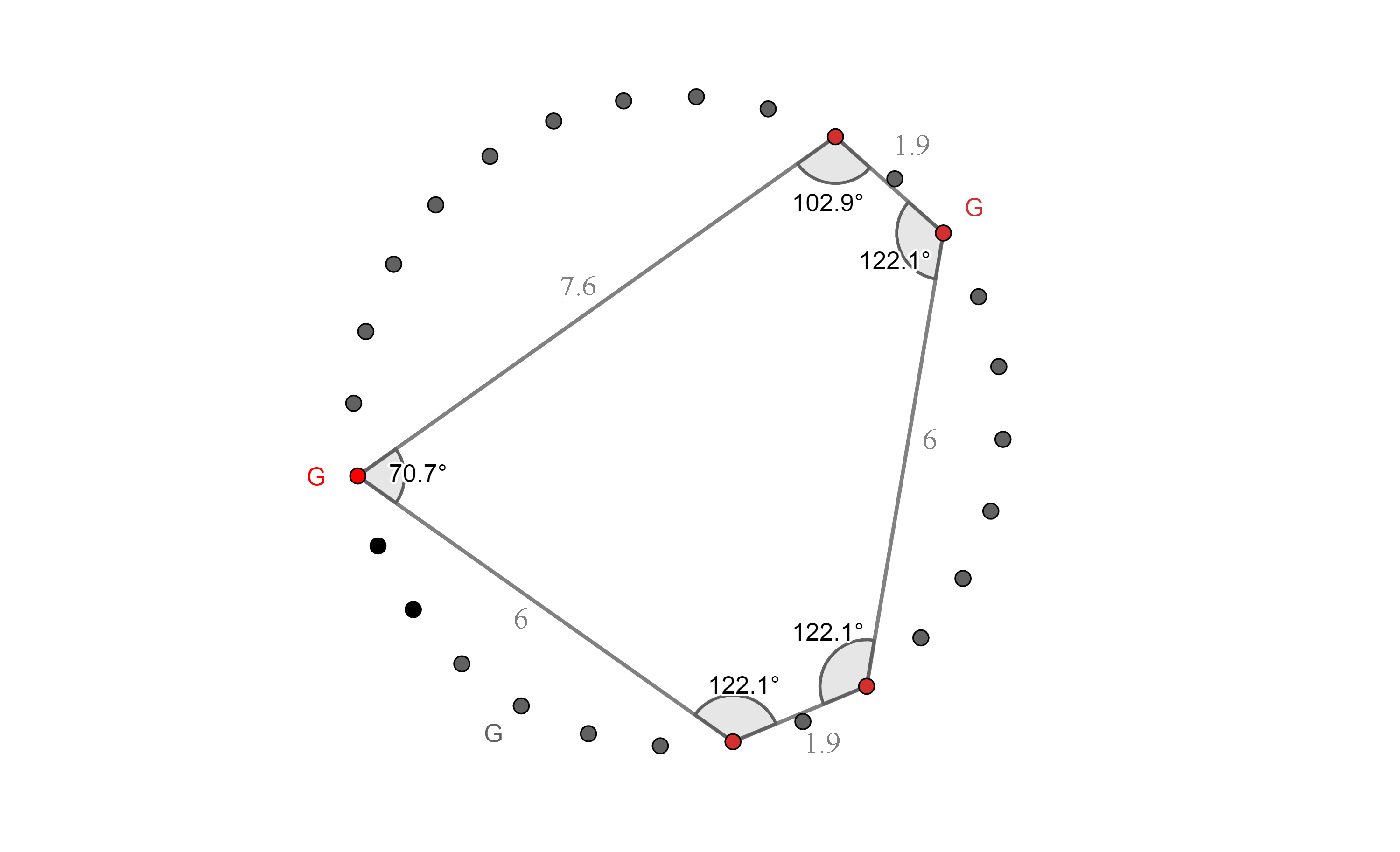
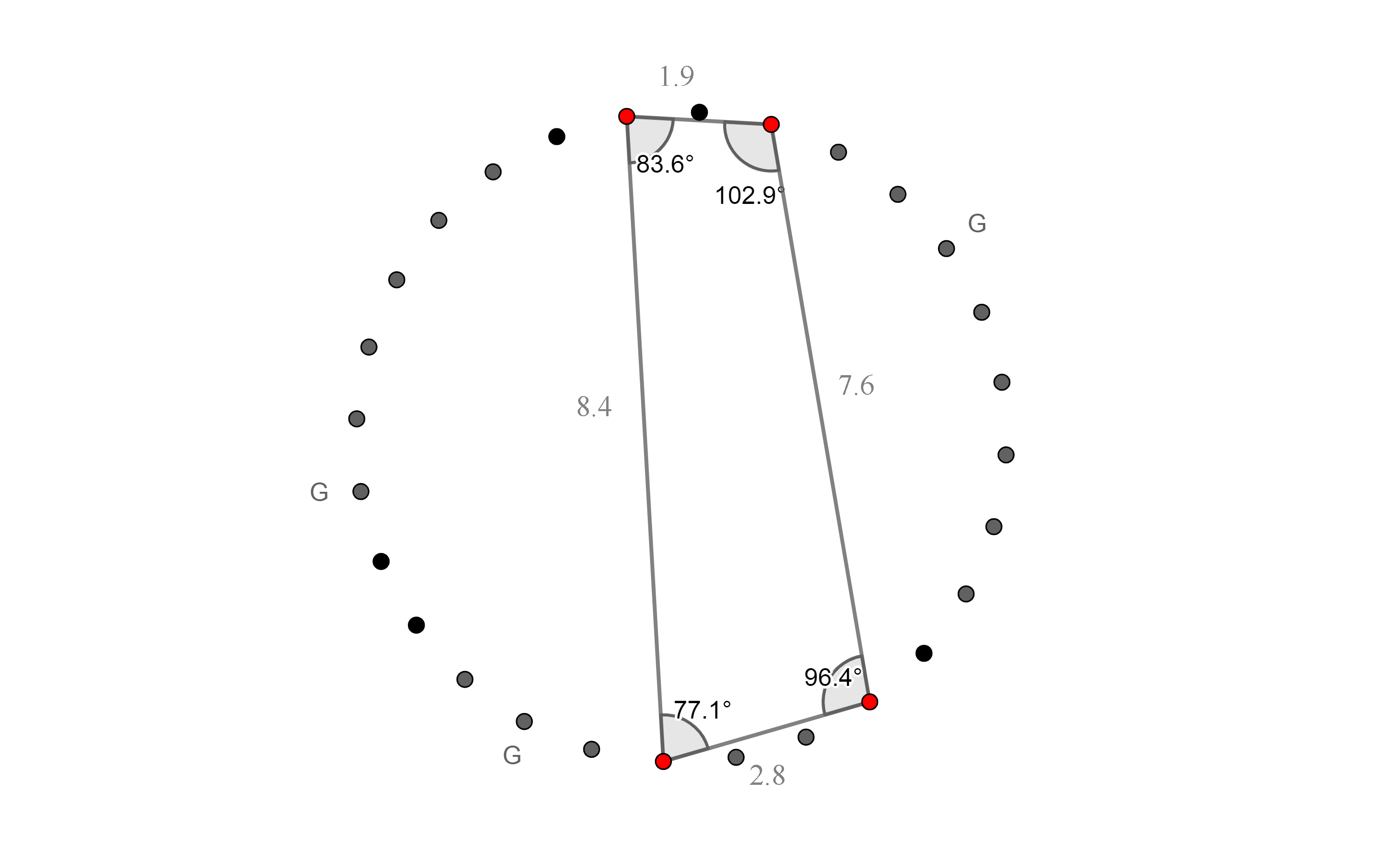
94. a, b ábrák
Az első ábra a 3. variáció harmadik ütemének a harmadik negyedéről
készült alakzata, amiben öt Hang vesz részt. Alulról felfelé: G, F,
G, D és E Hangok.
A második ábra a 3. és a 4. variáció első ütemének az első negyedéről
készült négyszöge. A Hangok: D, E, D és F. Azokon a helyeken, ahol a
kottakép megegyezik egymással, tehát a 3. és a 4. variációban a
harmadik ütem második negyedéig csak egy geometriai alakzatot építettem
fel. Az 5. és a 6. variációban ugyanígy jártam el.
A következő táblázatban feltüntetem az összes lehetséges területet
és a hozzá tartozó adatokat.
|
VARIÁCIÓ
|
ÜTEMSZÁM
|
AKKORD
SZÁM
|
HANGOK
|
TERÜLET
|
|
3 - 4
|
1
|
1
|
D, E, D, F
|
18,49
|
|
3 - 4
|
1
|
2
|
F, G, A, B
|
1,99
|
|
3 - 4
|
2
|
1
|
D, F, G, B, E
|
23,96
|
|
3 - 4
|
2
|
2
|
Cisz,
G, A, B, E
|
25,44
|
|
3 - 4
|
3
|
1
|
D, E, F, A, E
|
21,84
|
|
3 - 4
|
3
|
2
|
B, F, A, D, F
|
37,9
|
|
3
|
3
|
3
|
G, F, G, D, E
|
32,86
|
|
4
|
3
|
3
|
B,
E, G, Cisz, E
|
35,76
|
|
3
|
4
|
1
|
A, D, E, D
|
24,56
|
|
4
|
4
|
1
|
G,
A, F, G, D, E
|
38,55
|
|
3
|
4
|
2
|
E, G, Cisz
|
6,26
|
|
4
|
4
|
2
|
A, E, Cisz, D
|
24,53
|
|
3
|
4
|
3
|
A,
E, F, Cisz, A
|
35,26
|
|
5
|
1
|
1
|
D, D, E
|
7.88
|
|
6
|
1
|
1
|
D, E, F
|
0,49
|
|
5 - 6
|
1
|
2
|
F, G, A
|
0,8
|
|
5 - 6
|
1
|
3
|
D, F, B
|
4,97
|
|
5 - 6
|
2
|
1
|
Cisz, E, B
|
6,26
|
|
5 - 6
|
2
|
2
|
C, G, A
|
4,81
|
|
5 - 6
|
2
|
3
|
C, Fisz, A
|
6,26
|
|
5 - 6
|
3
|
1
|
H, F, G
|
4,07
|
|
5 - 6
|
3
|
2
|
B, Cisz, D, E
|
2,94
|
|
5
|
3
|
3
|
B, D, E
|
2,25
|
|
6
|
3
|
3
|
Gisz, D, E
|
4,07
|
|
5
|
4
|
1
|
A, H, F, G
|
9,68
|
|
6
|
4
|
1
|
A, D, F, G
|
10,65
|
|
5
|
4
|
2
|
Cisz, D, E, F
|
1,18
|
|
6
|
4
|
2
|
A,
H, Cisz, D, E
|
4,65
|
|
5
|
4
|
3
|
Cisz, E, G
|
2,4
|
|
6
|
4
|
3
|
A, G, Cisz
|
19,69
|
95. ábra
Az első sorba a variációk számát írtam, a második sor az ütemszámot
jelöli, a harmadik, az ütemen belüli alakzat számát, majd a következő
sorban a zenei Hangok nevét, amik a geometriai alakzatokat létrehozták
és az utolsó sorban pedig ezeknek az alakzatoknak a területét tüntettem
fel.
Összesen 30 darab alakzatot tudtam létrehozni, ebből háromnak
megegyezik a területe (6,26), illetve még kettőnek azonos (4,07). Így
elmondhatjuk, hogy 27 fajta területet számolhatunk össze. 27-72. A
27-es szám a Manduval köthető össze, a 72 pedig a Kerubokkal. A 30
darab alakzat a legkülönbözőbb szögeket zárta magába, amit eddig
sikerült megfejtenem, hogy 27 fajta szögből áll. 27 fajta szög, 27
fajta terület. Gondolom ez sem véletlen. A program, amivel dolgoztam a
geometriai alakzatok szerkesztésénél, nem szerkesztett teljes pontossággal,
csak tizedes jegyig mutatta a távolságokat, illetve a százados jegyek
alapján kerekítette a tizedes jegyeket. Ezáltal vannak kisebb
pontatlanságok, de a lényeg így is látszani fog.
Ezután nagyságrend szerint sorba raktam a területeket.
|
0,49
|
0,8
|
1,18
|
1,99
|
2,25
|
2,4
|
2,94
|
|
4,07
|
4,65
|
4,81
|
4,97
|
6,26
|
7,88
|
9,68
|
|
10,65
|
18,49
|
19,69
|
21,84
|
23,96
|
24,53
|
24,56
|
|
25,44
|
32,86
|
35,26
|
35,76
|
37,9
|
38,55
|
|
96. ábra
A kör, amiben megalkottam ezeket az alakzatokat, pontosan 8,5 átmérőjű,
tehát a sugara 4,25. Vagyis a kör területe 56,75-nek felel meg. Mivel a
területszámító program is csak két tizedesig számolt, úgy döntöttem,
hogy minden további értéket is két tizedesig számolok, hiszen a
pontatlanságok csak tovább növekednének.
A kör területének az aranymetszései:
56,75x 0,618=35,07
56,75x 0,382=21,67
A 96. ábrában pirossal jelölt kettő területtel rendelkező geometriai
alakzat, Hangcsoport, akkord a kör kisebbik és nagyobbik aranymetszése.
A kisebbik a 3. és 4. variáció harmadik ütemének az első negyede, a
nagyobbik pedig a 3. variáció utolsó (negyedik) ütemének harmadik
negyede, ő a befejező akkordja a 3. variációnak. A két aranymetszési
akkord közötti kottaanyag egy nagyon érdekes rész, ugyanis a Hangok,
az akkordok közötti különleges és igen bonyolult tükrözési ábrázolások
sorozata egy „mélyebb” világba vezet el bennünket, ami biztosan egy
külön fejezet témája lesz. Már elkezdtem vele foglalkozni, de amíg
frissek az aranymetszési sorozatban megtalált eredményeim, ezeket kell
leírnom.
Amit viszont már most fontosnak tartok, nézzük meg hányadik Helyen található
a 96. ábrán a két aranymetszés? 18 és 24. A Forrásnak pontosan 18 lépésre
van szüksége, mire egyszer körbejárja a Triászt. A 24 Vén, az
Univerzum Őrzői.
A következő táblázatban feltüntetem a 27 fajta terület aranymetszéseit.
|
|
TERÜLET
|
x
0,618
|
x
0,382
|
|
1
|
0,49
|
0,302
|
0,18
|
|
2
|
0,8
|
0,49
|
0,035
|
|
3
|
1,18
|
0,72
|
0,45
|
|
4
|
1,99
|
1,22
|
0,76
|
|
5
|
2,25
|
1,39
|
0,85
|
|
6
|
2,4
|
1,48
|
0,91
|
|
7
|
2,94
|
1,81
|
1,12
|
|
8
|
4,07
|
2,51
|
1,55
|
|
9
|
4,65
|
2,87
|
1,77
|
|
10
|
4,81
|
2,97
|
1,83
|
|
11
|
4,97
|
3,07
|
1,89
|
|
12
|
6,26
|
3,86
|
2,39
|
|
13
|
7,88
|
4,86
|
3,01
|
|
14
|
9,68
|
5,98
|
3,69
|
|
15
|
10,65
|
6,58
|
4,06
|
|
16
|
18,49
|
11,42
|
7,06
|
|
17
|
19,69
|
12,16
|
7,44
|
|
18
|
21,84
|
13,49
|
8,34
|
|
19
|
23,96
|
14,80
|
9,15
|
|
20
|
24,53
|
15,15
|
9,37
|
|
21
|
24,56
|
15,17
|
9,38
|
|
22
|
25,44
|
15,72
|
9,71
|
|
23
|
32,36
|
20,30
|
12,55
|
|
24
|
35,26
|
21,79
|
13,46
|
|
25
|
35,76
|
22,09
|
13,66
|
|
26
|
37,9
|
23,42
|
14,47
|
|
27
|
38,55
|
23,82
|
14,72
|
97. ábra
Az első sorban a terület száma található. Nagyságsorrendet vettem, később
lesz időrendi sor is! A kódfejtésnél több (rengeteg) lehetőség van
és ami csodálatossá teszi az egészet az, hogy ahány lehetőség,
annyi megfejtés, ha beavatott művel van dolgod. Csak legyen elég
gondolatod és tudásod mindent feltárni. Már most elárulhatom, hogy
erre csak a Teremtő képes! De azért jóérzéssel tölt el bennünket,
ha egy részét megfejtjük, hiszen annál közelebb kerülünk a Teremtőhöz
és nem utolsósorban okosodunk is.
A második sor a terület nagyságát, a harmadik sor a terület
aranymetszésének a nagyobbik, a negyedik sor pedig a kisebbik részét
tartalmazza.
Mint ahogyan korábban írtam minden adatnál csak két tizedesig írom a
számokat, de azért jobb ha tudjátok, hogy ezek közül is több szám
van, ami hasonlóan végtelen számot alkot, mint az aranymetszés arány
száma. Ez logikus és jó is. Ha majd lesz megfelelő technikai tudás,
mindenképpen teljes számsorokkal kell tovább számolni, a pontos
megfejtés miatt.
Vizsgáljuk meg az első 15 „terület” adatát és ezeknek az
aranymetszési számait. Minden számadathoz tartozik legalább egy másik
szám, a legtöbb esetben több szám. Párszor nulla, maximum 4 tized eltérés
van az egymáshoz tartozó számok között. A 4 csak két alkalommal
fordul elő, a 8. és a 14. számadatoknál, az összes többinél minimális
eltérésről beszélünk. Ezek érvényesek a területekre és mindkét
aranymetszési arányszámra. Vagyis nem marad ki egy számadat sem,
mindenkinek van társa, kapcsolata, egy egységben léteznek egymással.
A 16. helyen lévő adatokhoz már csak nyolc tizedes eltéréssel
kapcsolhatunk más számadatot, ez már mindenképpen soknak mondható, ő
„üresen” marad, tőle minden „messze” van.
Ezután következik 6 olyan terület (17, 18, 19, 20, 21 és 22), ahol
csak az aranymetszéseinek a kisebbik adatát lehet összekapcsolni a 13.
és a 14. számok területével (maximum 5 tized különbség).
Ezt követi a 23. szám, ahol a távolság már szintén nagynak mondható
(7 tized), üresen marad. Az utolsó 4 területnél (24, 25, 26 és 27)
pedig az aranymetszésének a nagyobbik száma köthető össze a 18. és
a 19. számok területével.
Ebben a kódban a világok egymáshoz való kapcsolódási viszonyait találhatjuk
meg.
Mi egy olyan világrendszerben élünk, ahol 16 párhuzamos univerzum van
egymás mellett, egymással összeköttetésben, pontosan ugyanúgy, mint
az első 16 „terület”. A párhuzamos univerzumok közötti utazás a
Nemtér- Nemidőn keresztül történik, ami nálunk ugye a 16. Hely, ahol
a távolság „messze” van a többi Helytől, ezért marad üresen. Itt
nem születik Világ, itt van a Káosz, erről a Helyről lehet a párhuzamos
világok egyikéből a másikba eljutni. Ha majd a jövőben valaki
kapcsolódási térképet készít a párhuzamos világok között, meggyőződésem,
hogy segítségére lesz a 97. ábrán feltüntetett számadataim.
Ez a rendszer a Téridőn belül keletkezik, amit az öt Atya hoz létre
hat Forráshelyen. Nálunk is megjelenik a hat Forráshely (17, 18, 19,
20, 21 és 22), aminek minden tagja, Forrása össze van kötve a párhuzamos
világok egyikével, pontosan a 13. és a 14. „világokkal” és ezáltal
az összes többivel.
Négy világrendszer van, ez volt az egyik. A mi világrendszerünkkel
ellen ütemben létezik egy tükör világ, ő a mihozzánk tartozó Antitér.
A Téridő születésénél létrejön egy tükör Téridő, ahol egy más
rendszerű világ jön létre mint a mi világunk és ők nagyol távol
vannak a mi párhuzamos univerzum rendszerünktől, az őhozzájuk való
utazásra egy másik Nemtér- Nemidő réteg tartozik, amin keresztül
lehetővé válik a térugrás. Ez a 97. ábrán a 23. Hely (terület). Az
utána levő négy fennmaradt „terület” jelöli a négy világot, világrendszert.
Mindegyik össze van kötve a Téridő Forrásaival, hiszen mindegyik
rendszer őbelőle jön létre. A hat Forráshelyből kettő Forráshely
van, itt nálunk ez a 18. és a 19. Hely (terület), ha egytől hatig számozzuk
a Téridő Forrásait, akkor a második és a harmadik Forráshely az,
ahol a mi világunk és a Téridő tükör Téridő világa találkozhat
(találkozik) egymással, illetve ezek azok a Forráshelyek, ahol a két
(négy, mivel mindkettőnek van egy anti-világa is) világrendszer között
kapcsolatot lehet teremteni, illetve átugrásra, átutazásra lehetőség
van. Itt azért még elég sok más számadatra is szükségünk lesz,
hiszen nem mindegy, hogy egy hozzánk hasonlatos világba jutunk, vagy az
antivilág részébe……
Fraktálvilág
A következő táblázatban megnézzük milyen arányban vannak egymással
a kör és a Hangcsoportok területei.
|
KÖR
|
TERÜLETEK
|
I. ARÁNY
|
II. ARÁNY
|
I. x 0,618
|
I. x 0,382
|
|
56,75
|
0,49
|
115,81
|
0,008
|
71,57
|
44,24
|
|
56,75
|
0,8
|
70,93
|
0,01
|
43,83
|
27,09
|
|
56,75
|
1,18
|
48,09
|
0,02
|
29,72
|
18,37
|
|
56,75
|
1,99
|
28,51
|
0,035
|
17,62
|
10,89
|
|
56,75
|
2,25
|
25,22
|
0,039
|
15,58
|
9,63
|
|
56,75
|
2,4
|
23,64
|
0,04
|
14,61
|
9,03
|
|
56,75
|
2,94
|
19,30
|
0,05
|
11,92
|
7,37
|
|
56,75
|
4,07
|
13,94
|
0,07
|
8,61
|
5,32
|
|
56,75
|
4,65
|
12,20
|
0,081
|
7,54
|
4,66
|
|
56,75
|
4,81
|
11,79
|
0,084
|
7,29
|
4,50
|
|
56,75
|
4,97
|
11,41
|
0,087
|
7,05
|
4,36
|
|
56,75
|
6,26
|
9,06
|
0,11
|
5,60
|
3,46
|
|
56,75
|
7,88
|
7,20
|
0,13
|
4,45
|
2,75
|
|
56,75
|
9,68
|
5,86
|
0,17
|
3,62
|
2,23
|
|
56,75
|
10,65
|
5,32
|
0,18
|
3,29
|
2,03
|
|
56,75
|
18,49
|
3,06
|
0,32
|
1,89
|
1,17
|
|
56,75
|
19,69
|
2,88
|
0,34
|
1,78
|
1,10
|
|
56,75
|
21,84
|
2,59
|
0,38
|
1,60
|
0,99
|
|
56,75
|
23,96
|
2,36
|
0,42
|
1,46
|
0,90
|
|
56,75
|
24,53
|
2,313
|
0,4322
|
1,429
|
0,883
|
|
56,75
|
24,56
|
2,310
|
0,4327
|
1,427
|
0,882
|
|
56,75
|
25,44
|
2,23
|
0,44
|
1,37
|
0,85
|
|
56,75
|
32,84
|
1,72
|
0,57
|
1,06
|
0,65
|
|
56,75
|
35,26
|
1,60
|
0,62
|
0,98
|
0,61
|
|
56,75
|
35,76
|
1,58
|
0,63
|
0,97
|
0,60
|
|
56,75
|
37,9
|
1,49
|
0,66
|
0,92
|
0,57
|
|
56,75
|
38,55
|
1,47
|
0,67
|
0,90
|
0,56
|
98. ábra
Itt is mindent kettő tizedesig írok, de az összes szám sokkal
hosszabb. Az első oszlopban a kör területe található, ami egy állandó
szám, de csak azért, mert a teremtés egy pillanatát elemzem, bemutatva
az összefüggéseket. A második oszlopban a Hangcsoportok területeit
találjuk a legkisebb területtel elkezdve a legnagyobb területig. A
harmadik oszlopban a kör és a hozzátartozó terület viszonyát vizsgáljuk,
a Hangcsoportok területét elosztjuk a kör területével, vagyis megnézzük
hányszor fér a körbe ez a terület (pl. 56,76: 0,49=115,81). A negyedik
oszlop ennek az ellentéte (0,49: 56,76= 0,008 . .). Az ötödik oszlop a
harmadik oszlopban szereplő összegnek az aranymetszése, méghozzá a
nagyobbik része. Az utolsó oszlop pedig a harmadik oszlopban szereplő
szám aranymetszésének a kisebbik része. Összehasonlítva a harmadik,
az ötödik és a hatodik oszlopban szereplő számokat az tűnik fel,
hogy minimális eltéréssel egymással azonos adatokat fedezünk fel
legalább egyszer, de inkább többször. Természetesen a legnagyobb értéknek
nincsen párja (115,81), vagy legalábbis itt nincsen párja, hiszen őbelőle
indultunk ki. Kettő összegnél van nagyobb távolság (négy egész), a
48-hoz a 44 és 43, illetve 23-hoz a 27. A pirossal jelölt Hangcsoportok
területeinek száma a kör aranymetszései. A körrel kijött viszonyítási
számok és ezeknek aranymetszés adatai egy fontos összefüggést
mutatnak. A 2,59-es számadat nagyobbik aranymetszése az 1,60, ami a kör
kisebbik aranymetszési területének (21,84) a viszonyítási száma a kör
és a terület között (1,60). Az 1,60-os szám aranymetszésének a
kisebbik része (0,61) „megegyezik” a kör aranymetszés nagyobbik részének
(35,26) a hozzávaló viszonyítási összegével (0,62). Ez itt a fordulópont,
ahol egyértelműen kiderül, hogy egy teljesen precíz egymásba fordulásos
mozgásról van szó, ahol az arányok egymás aranymetszési arányaiban
történnek meg, harmonizálódnak. A táblázatban megjelenített értékek
még egy pillanat „hosszáig” sem tartanak, hiszen a létezésben
minden változik, minden változásban van, de ez a változás a
legnagyobb rendben, a legnagyobb harmóniában történik, ahol az egyik
legfontosabb szabály az aranymetszési arány érvényesülése.
Amikor egy Létezés megszületik (Hangcsoportok területei), az őbelőle
kiáradó hullámterek a saját maga létezési információjukkal ellátva
addig terjednek minden irányba (területek többszörösei), amíg a Téridő
tart (a kör határáig). Ennek a táblázatnak az adatai a fraktálvilág
keletkezésének az első lépéseit mutatják be.
Ennek a fejezetnek az utolsó részéhez érkeztem, ami nem azt jelenti,
hogy ebben a négy variációban nincsen több felfedezni való. Ellenkezőleg.
Ez csak a kezdete az aranymetszési láncolatok megtalálásának, a fraktálokból
felépülő világ létrejöttének. Minél tovább megyünk egy úton,
annál több elágazás képződik anélkül, hogy az eredeti anyagot megváltoztattuk
volna. Őbelőle jött létre minden, az ő információs tartományában
van minden.
A 30 eredeti területet most sorban, ahogyan a kottában van (a megegyező
kottaképi Hangcsoportokat csak egyszer) mutatom meg más összefüggésben.
A 95. ábra alapján be tudjátok azonosítani a Hangcsoportokat, a területeket
és a Helyüket a kottában.
|
TERÜLET SZÁMA
|
TERÜLET
|
TERÜLET
ARANYMETSZÉSEIHEZ LEGKÖZELEBB
ÁLLÓ TERÜLETEK
|
SZÖGEK
|
|
1
|
18,49
|
Nemtér-Nemidő
|
|
|
2
|
1,99
|
16, 27
|
30°,
84°, 66°
|
|
3
|
23,96
|
25
|
|
|
4
|
25,44
|
25
|
|
|
5
|
21,84
|
14
|
|
|
6
|
37,9
|
3
|
|
|
7
|
32,86
|
Nemtér-Nemidő
|
|
|
8
|
35,76
|
5
|
|
|
9
|
24,56
|
25
|
|
|
10
|
38,55
|
3
|
|
|
11
|
6,26
|
21, 24, 29 (25,
26)
|
54°, 102°, 126°, 78°
|
|
12
|
24,53
|
25
|
|
|
13
|
35,26
|
5
|
|
|
14
|
7,88
|
22, 28
|
36°, 48°, 96°
|
|
15
|
0,49
|
16 (27)
|
|
|
16
|
0,8
|
2, 15, 23, 27 (29)
|
114°, 126°, 72°, 132°,
96°
|
|
17
|
4,97
|
2, 22 (19)
|
90°, 60°, 30°
|
|
18
|
6,26
|
21, 24, 29 (25,
26)
|
48°, 144°, 132°, 36°
|
|
19
|
4,81
|
2, 22
|
60°, 102°, 18°
|
|
20
|
6,26
|
21, 24, 29 (25,
26)
|
48°, 156°, 132°, 24°
|
|
21
|
4,07
|
27, 29
|
12°, 126°, 42°
|
|
22
|
2,94
|
2, 27 (17,
19)
|
30°, 120°, 30°
|
|
23
|
2,25
|
16, 27 (2,
24, 29)
|
24°, 114°, 42°
|
|
24
|
4,04
|
27, 29
|
12°, 150°, 18°
|
|
25
|
9,68
|
11,
18, 20, 21, 24
|
42°,
126°, 162°, 156°, 156°, 78°
|
|
26
|
10,65
|
11,
18, 20, 21, 24
|
48°,
126°, 162°, 156°, 150°, 78°
|
|
27
|
1,18
|
15, 16
(2, 23)
|
108°, 66°, 6°
|
|
28
|
4,65
|
2, 22
(19)
|
24°, 120°, 36°
|
|
29
|
2,4
|
27
(16, 23)
|
|
|
30
|
19,69
|
14
|
|
99. ábra
Az első oszlopban a területek sorszámát találjuk, a másodikban magát
a területet. A harmadik oszlopban a terület aranymetszéseihez legközelebb
álló területek sorszámát tüntettem fel. Ez itt most az elsődleges
kapcsolat. Két helyen a Nemtér-Nemidő található, amit a 97. ábra
alatti részben fejtettem ki. Ahol egy szám van, ott a területnek csak
az egyik aranymetszési arányát lehetett megtalálni, ahol két szám
van ott mindkét arány elérhető volt és ahol több szám van, ott több
lehetőséget találtam. A zárójelbe tett területsorszámok már egy második
lépcsőzési szinthez vezetnek, ahol az aranymetszési adatokhoz a hozzá
legközelebb álló aranymetszési adatok területi sorszámát írtam oda
(ezeket itt már nem elemeztem tovább). A harmadik lépés lenne az, hogy
minden számot feltüntetni abban a sorban, ahol már egyszer szerepelt,
mint például a 6-os sorszámú terület elsődleges kapcsolata a 3-as
terület, de a 3-as területnél ebben a táblázatban nem jelenik meg a
6-os kapcsolat. Ha minden kapcsolatot oda vissza és még lenne egy pár
ötletem hogyan mit kapcsoljunk egymáshoz, olyan bonyolult lenne hirtelen
a rendszer, hogy senki nem ismerné ki magát rendesen. Lépésről lépésre
érdemes haladni.
A negyedik oszlopban szögeket tüntettem fel. Azokon a helyeken, ahol több
mint kettő számkapcsolat jött létre (ahogyan már írtam, a zárójelbe
tett számokat itt nem használom), mindegyikből geometriai ábrákat
hoztam létre. 30 pontból álló kört alkottam (30 terület, 30 pont)
egymástól egyenlő távolságra és a megfelelő területszámokat összekötve
különböző alakzatokat kaptam. A pirossal jelölt számok a korábban
kifejtett két aranymetszési Helye a „körnek”.
Az alakzatok szögei egy 6-os rendszert hoztak létre. A táblázatunk
alapján 16 alakzatot hozhatunk létre, ami a párhuzamos világok száma.
Ezenkívül még szerkesztettem két ábrát, az egyik a három egyforma
területű terület sorszámából (6,26-ból 11, 18 és 20), a másik
pedig a kör aranymetszési kapcsolatából (5, 13, 14 és 8). Ez utóbbit
be is mutatom másik kettő kíséretében.

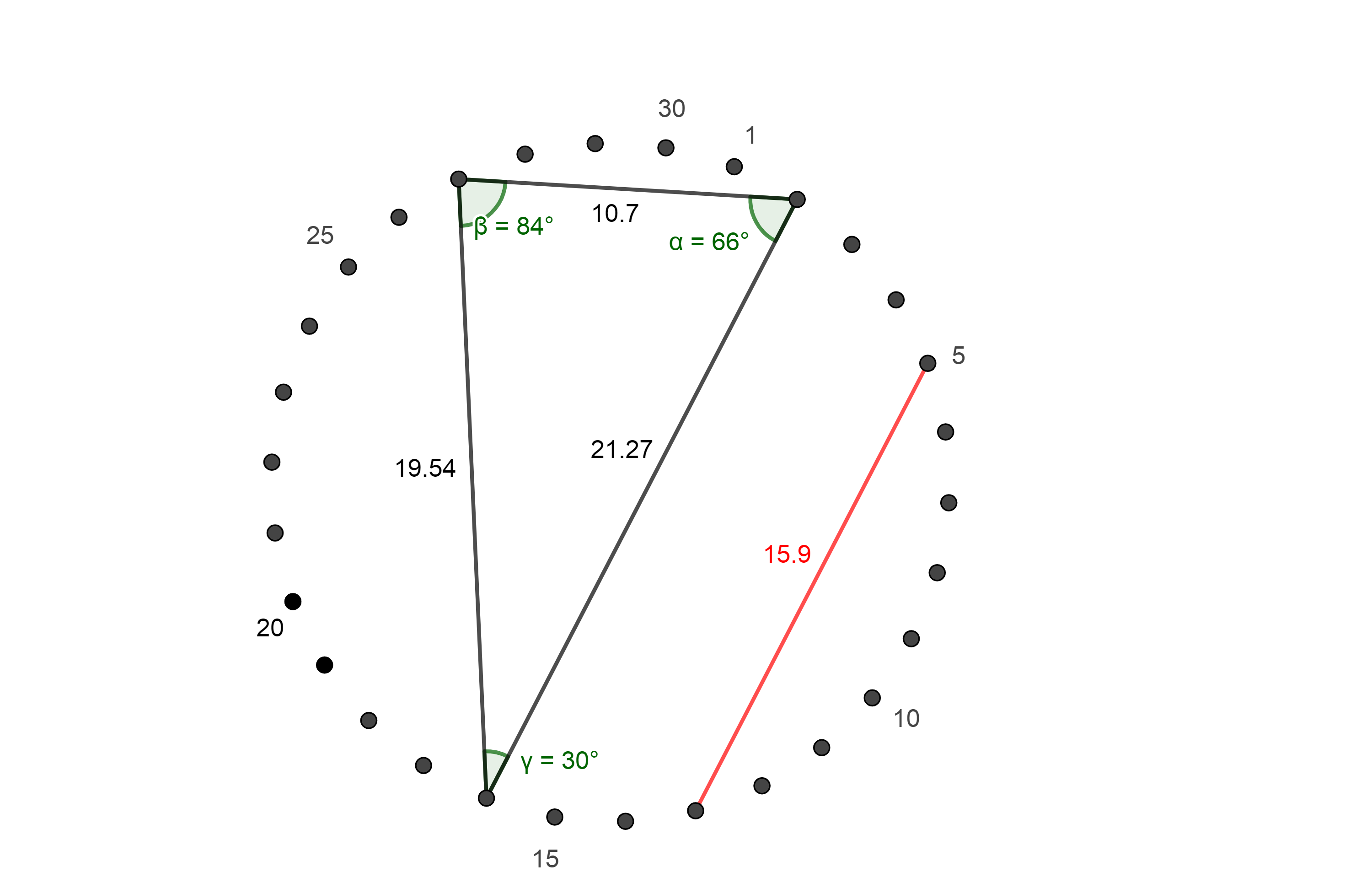
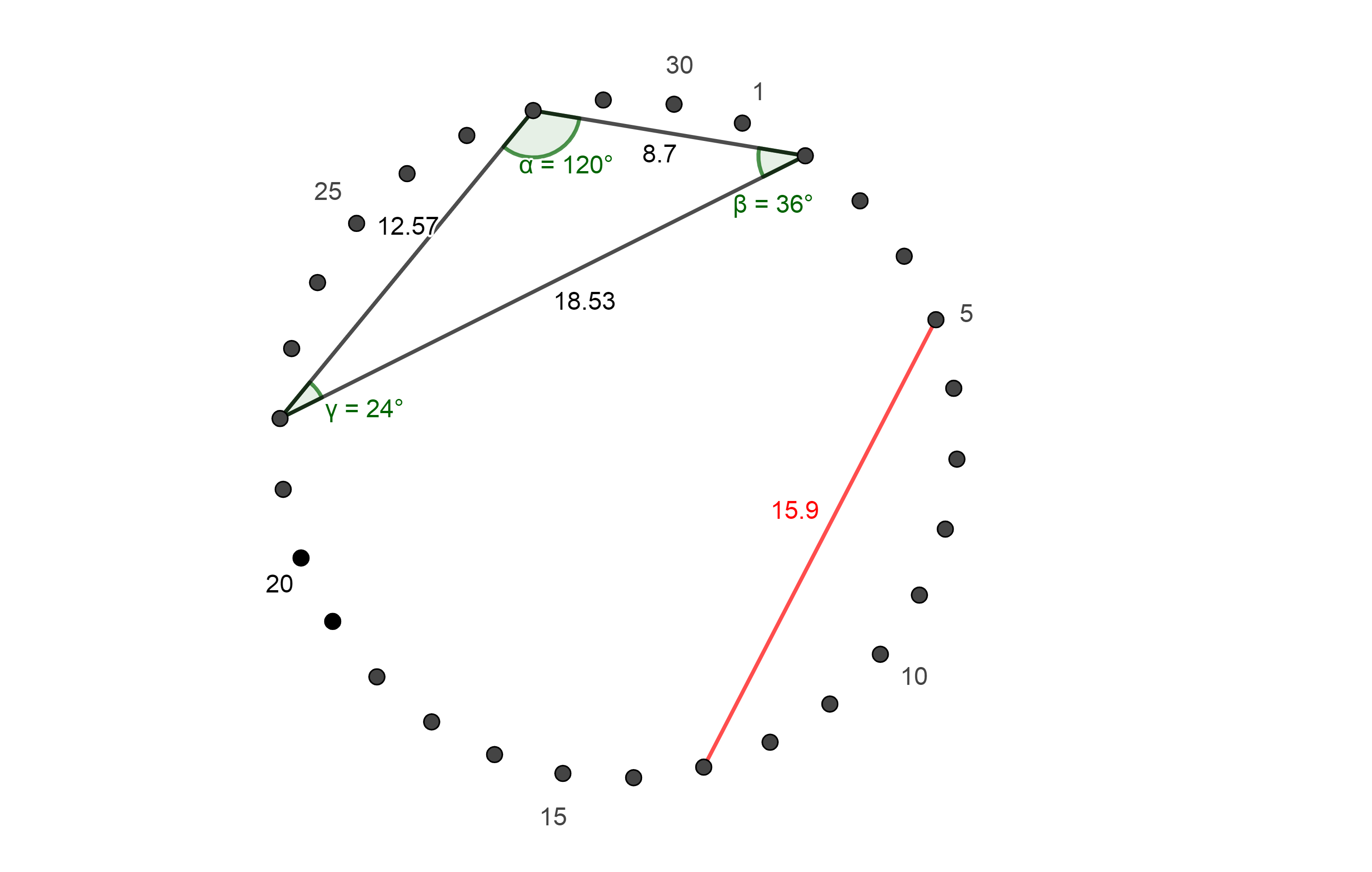
100. a, b, c ábrák
A piros vonal az 5. és a 13. területet köti össze. Ez a két
aranymetszési adata a körnek. Az 5. és a 14. pontok összekötésével
kapunk egy 6-os szöget. A 8. ponttal való összekötés után létrejön
egy 30-as és egy 36-os szög. 30:6=5 és 36:6=6
A Téridő létrejöttében 6 Forráshely vesz részt, amelyekben az öt
Atya lépésről lépésre halad úgy, hogy minden Forráshelyen mind az
öt Atya áthalad, de egy Forráshely mindig üresen marad, így léteztetik
egymást. Ezt mondja el ez az ábra.
A következő ábra szögei: 84, 66 és 30.
Az aranymetszési piros vonalat meghagytam minden ábrámnál, hiszen ez
is egy kutatási terület, milyen viszonyban vannak egymással az
alakzatok és a piros vonal.
Az aranyszög, ami az egyik legfontosabb arányt mutatja az élővilág
fejlődésében kb. 137,5 szöget zár be (egyébként ez is végtelen szám).
137,5 x 0,618= 84,975
Tehát az egyik szögünk, a 84 megfelel az aranyszög aranymetszése
nagyobbik arányának. Egy másik ötlet: a Ji Csing táblázatban az élet-halál
helye, a fordulópont a 42-21-nél van. Itt feleződés van, a többi
helyen többszöröződnek a számok. 84-nek a fele 42, így a 21-es szám
is többszörösen megvan benne.
A 66-os szám Jézus titkos száma, de elosztva 6-tal 66:6=11 megkapjuk az
egyhiperteres Téridő számát.
A 30-as szám lehet az öt Forráshely, 30:6=5
De lehet a Teremtő sebessége is, ahol már a teremtés megkezdődött és
most is folyamatosan zajlik, RV=3,16
A harmadik ábra szögei: 24, a Vének száma, 36:6=6 a Téridő Forráshelyeinek
száma és 120:6=20 pedig az aminosavak száma, akik a szénalapú élet
megalapozói.
Minden szög, ami ebben a rendszerben létrejött osztható hattal, a Téridő
Forráshelyeinek a számával és minden eredmény elmond valamit a Téridőben
keletkezett létezésről és önmagában is ad egy másik adatot. Ez a
rendszer már a Téridőben „játszódik”. 6-162-ig megtalálható
minden hattal osztható szám egyetlen egyet kivéve a 138-as számot. Ez
a legközelebbi szög (ebben a rendszerben ő jelenti) az aranyszöghöz.
Az, hogy miért ez a szög hiányzik, még rejtély számomra. Az így összeszámolt
szögek fajtája 26+1=27
Egyébként nagyon valószínűnek tartom, hogy a 6-os szögek sorozata
komoly összefüggéseket mutat a biológiai világ kialakulásában és létezésében.
Folytatás jön.
|